Toán học giả thuyết Riemann

Giả thuyết Riemann, trong lý thuyết số, giả thuyết của nhà toán học người Đức Bernhard Riemann liên quan đến vị trí của các giải pháp cho hàm Riemann zeta, được kết nối với định lý số nguyên tố và có ý nghĩa quan trọng đối với việc phân phối các số nguyên tố. Riemann đã đưa ra giả thuyết trong một bài báo, Hồi Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse ((Về số lượng số ít hơn một số lượng nhất định của Học viện Berlin Berlin).

Hàm zeta được định nghĩa là chuỗi vô hạn ζ (s) = 1 + 2 ^s + 3 ^s + 4 ^s +, hoặc, trong ký hiệu nhỏ gọn hơn, , trong đó tổng (Σ) số hạng của n chạy từ 1 đến vô cực thông qua các số nguyên dương và s là một số nguyên dương cố định lớn hơn 1. Hàm zeta được nghiên cứu đầu tiên bởi nhà toán học Thụy Sĩ Leonhard Euler trong thế kỷ 18. (Vì lý do này, đôi khi nó được gọi là hàm zuler Euler. Đối với ζ (1), chuỗi này chỉ đơn giản là chuỗi điều hòa, được biết đến từ thời cổ đại để tăng mà không bị ràng buộc, tức là tổng của nó là vô hạn. đã chứng minh vào năm 1735 rằng ζ (2) = π ^2/6, một vấn đề đã lảng tránh các nhà toán học vĩ đại nhất của thời đại, bao gồm cả gia đình Bernoulli của Thụy Sĩ (Jakob, Johann và Daniel). Tổng quát hơn, Euler đã phát hiện ra (1739) mối quan hệ giữa giá trị của hàm zeta đối với các số nguyên chẵn và các số Bernoulli, là các hệ số trong khai triển chuỗi Taylor của x / (e ^x - 1). (Xem thêm hàm số mũ.) Vẫn còn tuyệt vời hơn, vào năm 1737 Euler đã phát hiện ra một công thức liên quan đến hàm zeta, bao gồm tổng hợp một chuỗi các thuật ngữ vô hạn chứa các số nguyên dương và một sản phẩm vô hạn liên quan đến mọi số nguyên tố:

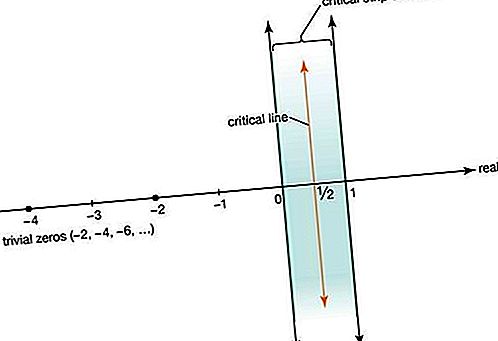
Riemann đã mở rộng nghiên cứu về hàm zeta để bao gồm các số phức x + iy, trong đó i = Căn bậc hai của √ 1, ngoại trừ dòng x = 1 trong mặt phẳng phức. Riemann biết rằng hàm zeta bằng 0 đối với tất cả các số nguyên âm chẵn 2, −4, 6,

(được gọi là số không tầm thường) và nó có số lượng số không vô hạn trong dải số phức quan trọng nằm giữa các dòng x = 0 và x = 1. dòng quan trọng x = ¹ / ₂. Riemann phỏng đoán rằng tất cả các số không không có giá trị đều nằm trên đường giới hạn, một phỏng đoán mà sau đó được gọi là giả thuyết Riemann.

Năm 1914 nhà toán học tiếng Anh Godfrey Harold Hardy đã chứng minh rằng một số vô hạn các giải pháp của ζ (s) = 0 tồn tại trên dòng quan trọng x = ¹ / ₂. Sau đó, các nhà toán học khác nhau đã chỉ ra rằng một tỷ lệ lớn các giải pháp phải nằm trên đường giới hạn, mặc dù các bằng chứng thường xuyên về bằng chứng là tất cả các giải pháp không cần thiết đều bị sai sót. Máy tính cũng đã được sử dụng để thử nghiệm các giải pháp, với 10 nghìn tỷ giải pháp không cần thiết đầu tiên được hiển thị nằm trên đường giới hạn.

Một bằng chứng về giả thuyết Riemann sẽ có những hậu quả sâu rộng đối với lý thuyết số và cho việc sử dụng các số nguyên tố trong mật mã học.

Giả thuyết Riemann từ lâu đã được coi là vấn đề chưa được giải quyết lớn nhất trong toán học. Đó là một trong 10 vấn đề toán học chưa được giải quyết (23 trong địa chỉ in) được đưa ra như một thách thức đối với các nhà toán học thế kỷ 20 của nhà toán học người Đức David Hilbert tại Đại hội toán học quốc tế lần thứ hai ở Paris vào ngày 8 tháng 8 năm 1900. Năm 2000 nhà toán học người Mỹ Stephen Smale cập nhật ý tưởng của Hilbert với một danh sách các vấn đề quan trọng trong thế kỷ 21; giả thuyết Riemann là số một. Năm 2000, nó đã được chỉ định là một vấn đề thiên niên kỷ, một trong bảy vấn đề toán học được lựa chọn bởi Viện toán học Clay của Cambridge, Mass., US, cho một giải thưởng đặc biệt. Giải pháp cho mỗi Vấn đề Thiên niên kỷ trị giá 1 triệu đô la. Năm 2008, Cơ quan Dự án Nghiên cứu Tiên tiến Quốc phòng Hoa Kỳ (DARPA) đã liệt kê nó là một trong những Thách thức Toán học của DARPA, 23 vấn đề toán học mà nó đang thu hút các đề xuất nghiên cứu để tài trợ cho Thử thách Toán học của Thằng Nineteen: Giải quyết Giả thuyết Riemann. Chén Thánh của lý thuyết số.