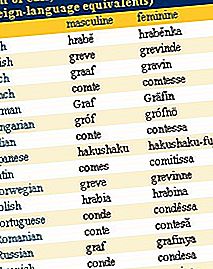
Hoán vị và kết hợp, các cách khác nhau trong đó các đối tượng từ một tập hợp có thể được chọn, nói chung mà không cần thay thế, để tạo thành các tập hợp con. Lựa chọn tập hợp con này được gọi là hoán vị khi thứ tự lựa chọn là một yếu tố, sự kết hợp khi thứ tự không phải là một yếu tố. Bằng cách xem xét tỷ lệ số lượng các tập con mong muốn với số tập hợp con có thể có trong nhiều trò chơi may rủi trong thế kỷ 17, các nhà toán học người Pháp Blaise Pascal và Pierre de Fermat đã thúc đẩy sự phát triển của tổ hợp và lý thuyết xác suất.
tổ hợp: hệ số nhị thức
n đối tượng được gọi là hoán vị của n thứ lấy r tại một thời điểm. Số lượng hoán vị là
Các khái niệm và sự khác biệt giữa hoán vị và kết hợp có thể được minh họa bằng cách kiểm tra tất cả các cách khác nhau trong đó một cặp đối tượng có thể được chọn từ năm đối tượng có thể phân biệt được như các chữ cái A, B, C, D và E. Nếu cả hai các chữ cái được chọn và thứ tự lựa chọn được xem xét, sau đó 20 kết quả sau đây là có thể:

Mỗi trong số 20 lựa chọn có thể khác nhau này được gọi là hoán vị. Cụ thể, chúng được gọi là hoán vị của năm đối tượng lấy hai lần và số lượng hoán vị có thể được biểu thị bằng ký hiệu 5 P 2, đọc Lát 5 hoán vị 2. Nghi Nói chung, nếu có n đối tượng có sẵn để chọn và hoán vị (P) sẽ được hình thành bằng cách sử dụng k của các đối tượng tại một thời điểm, số lượng hoán vị khác nhau có thể được biểu thị bằng ký hiệu n P k. Một công thức để đánh giá của nó là n P k = n! / (N - k)! Biểu thức n! Giành đọc và thực tế là tính toán. Tất cả các số nguyên dương liên tiếp từ 1 đến và bao gồm n sẽ được nhân với nhau, và 0! được định nghĩa bằng 1. Ví dụ: sử dụng công thức này, số lượng hoán vị của năm đối tượng được thực hiện hai lần là

(Với k = n, n P k = n! Do đó, đối với 5 đối tượng có 5! = 120 sắp xếp.)
Đối với các kết hợp, k đối tượng được chọn từ một tập hợp n đối tượng để tạo tập hợp con mà không cần đặt hàng. Đối chiếu ví dụ hoán vị trước đó với sự kết hợp tương ứng, các tập hợp con AB và BA không còn là các lựa chọn khác biệt; bằng cách loại bỏ các trường hợp như vậy, chỉ còn lại 10 tập hợp con có thể khác nhau AB, AC, AD, AE, BC, BD, BE, CD, CE và DE.
Số lượng các tập con như vậy được ký hiệu là n C k, đọc Số n chọn k. Đối với kết hợp, vì k đối tượng có k! Sắp xếp, có k! hoán vị không thể phân biệt cho mỗi lựa chọn của k đối tượng; do đó chia công thức hoán vị cho k! mang lại công thức kết hợp sau:
Điều này giống như hệ số nhị thức (n, k) (xem định lý nhị thức). Ví dụ: số lượng kết hợp của năm đối tượng được thực hiện hai lần là
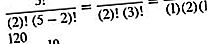
Các công thức cho n P k và n C k được gọi là các công thức đếm vì chúng có thể được sử dụng để đếm số lượng hoán vị hoặc kết hợp có thể có trong một tình huống nhất định mà không phải liệt kê tất cả.